腾讯云
visual studio
web
react.js
binder
寒武纪面试
SylixOS
collections
gcc
diffusion model
cnn
.net
java8新特性
websocket
ras
考试管理系统
webrtc
SpringMVC的常见注解
微信授权功能
skill command
零知识证明
2024/4/11 18:29:17椭圆曲线介绍(一):实数上面的椭圆曲线
大部分内容翻译自 ANDREA CORBELLINI的椭圆曲线密码学的介绍:Elliptic Curve Cryptography: a gentle introduction 我在里面加了一些使用python绘制椭圆曲线的方法,可以复制代码下来自行尝试。 文章目录前言实数和群内的椭圆曲线椭圆曲线椭圆曲线群几何…
4+机器学习+实验验证
今天给同学们分享一篇4机器学习实验验证的生信文章“Identification and Analysis of Neutrophil Extracellular Trap-Related Genes in Osteoarthritis by Bioinformatics and Experimental Verification”,这篇文章于2023年8月31日发表在 J Inflamm Res 期刊上&am…
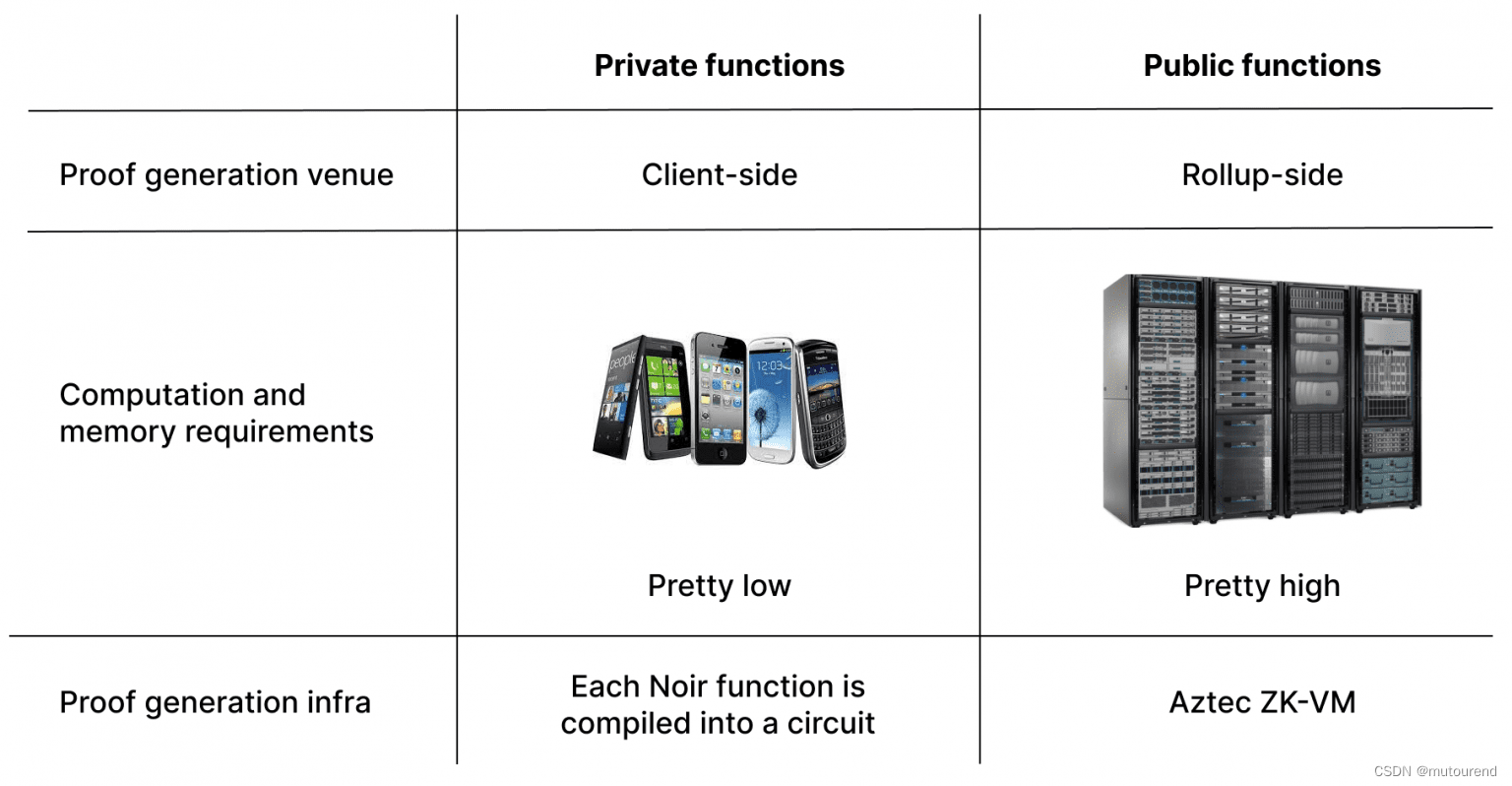
Aztec的客户端证明
1. 引言
隐私保护 zk-rollup 的证明生成与通用 zk-rollup 的证明生成有很大不同。原因是给定交易中存在特定数据(由私有函数处理),我们希望保持完全私有。在本文中,我们探讨了用于证明私有函数正确执行的客户端证明生成ÿ…
零知识证明从0到1,ZK简介
文章目录ZK简介例子承诺协议如何证明零知识性质如何证明任意的statement证明和证明某个知识由Schnorr身份认证协议来看看ZK的性质,以及如何转为非交互式证明completenessSoundnessZero-knowledgeness从交互式证明到非交互式三种基础ZK:SNARKS,…
NFT数字藏品交易平台免费版源码-视觉猿CMS
下载链接在文章尾部
系统介绍 后台截图 一、视觉猿CMS数字藏品交易系统特色功能
1、数字藏品铸造
提供数字藏品全自动上链并且在链上存证的唯一性身份。
2、数字藏品销售/盲盒/购买
提供数字藏品多样性销售,可以销售数字藏品和盲盒,单人购买数量可以限制,增加抢购热情,…
ZKP3.2 Programming ZKPs (Arkworks Zokrates)
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 3: Programming ZKPs (Guest Lecturers: Pratyush Mishra and Alex Ozdemir)
3.3 Using a library ( tutorial)
R1CS Libraries A library in a host language (Eg: Rust, OCaml, C, Go, …)Key type: constraint system Mai…
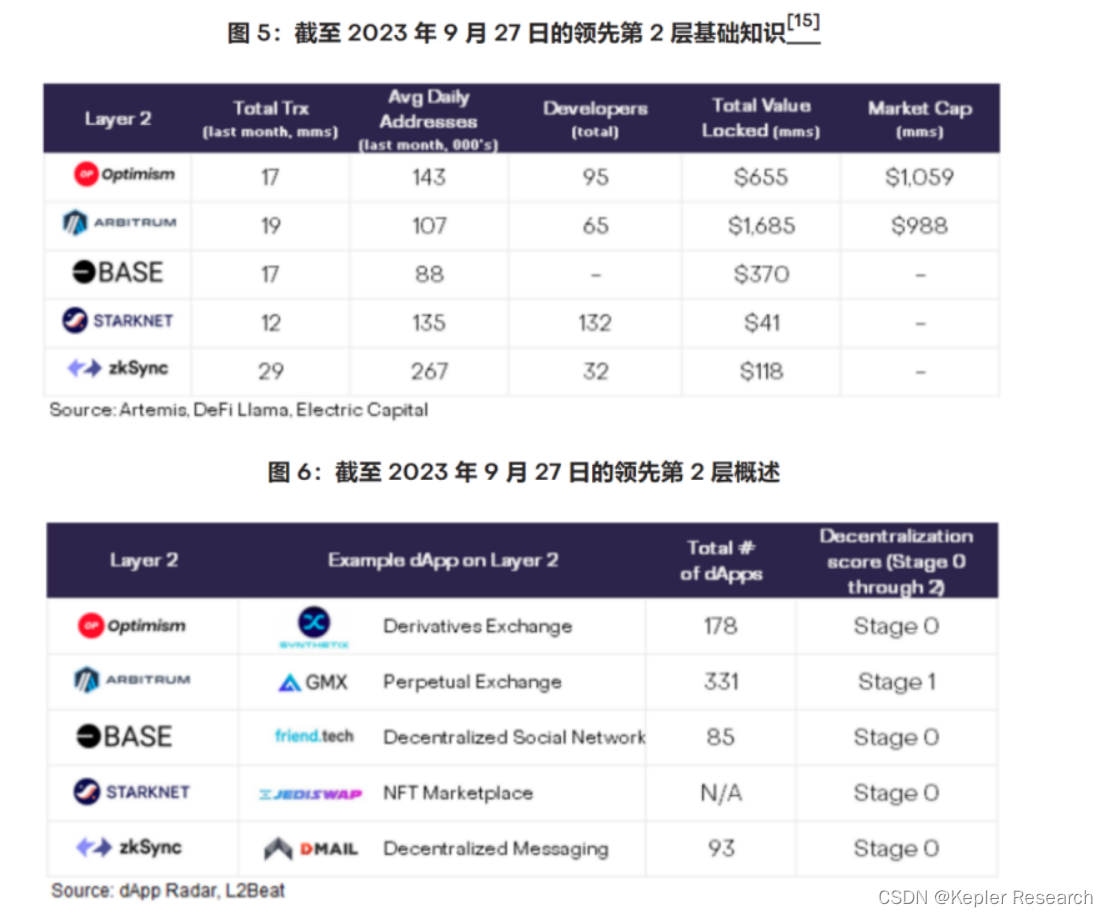
Layer 2:百倍利润无限可能的首选赛道
截至 2023 年 9 月,以太坊在过去一年中上涨了 22%,表现优于大多数大型智能合约区块链。第 2 层 (L2) 在推动以太坊价值方面发挥了重要作用。 Layer 2 可以增强以太坊的可扩展性,使用户的网络成本降低 100 倍。 Coinbase 于 8 月推出了 BASE…
5+甲基化+预后模型搭配实验
今天给同学们分享一篇甲基化预后模型实验的生信文章“Six immune-related promising biomarkers may promote hepatocellular carcinoma prognosis: a bioinformatics analysis and experimental validation”,这篇文章于2023年3月23日发表在Cancer Cell Int期刊上&…
4+内质网应激+预后模型教你如何应用到自己的生信分析研究中。
今天给同学们分享一篇内质网应激预后模型的生信文章“Characteristics of endoplasmic reticulum stress in colorectal cancer for predicting prognosis and developing treatment options”,这篇文章于2023年3月31日发表在Cancer Med期刊上,影响因子为…
零知识证明(zk-SNARK)(二)
From Computational Problem to zk-SNARK
本部分就是将计算难题转换为多项式,然后使用zk-SNARK。 (注:以下用 P,V 替代 Prover,Verifier)
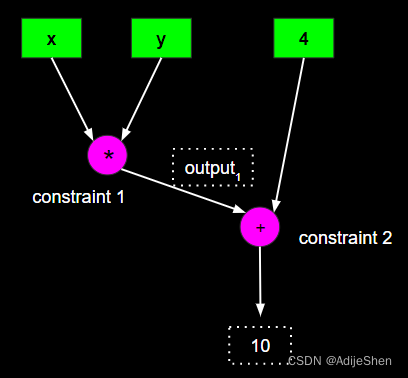
计算难题->R1CS
R1CS(Rank-1 Constraint System)是一种能够…
基于cycle of curves的Nova证明系统
1. 引言
主要见斯坦福大学Wilson Nguyen、Dan Boneh和微软研究中心Srinath Setty 2023年论文《Revisiting the Nova Proof System on a Cycle of Curves》。
前序博客有:
Nova: Recursive Zero-Knowledge Arguments from Folding Schemes学习笔记
在2021年Nova …
基于cycle of curves的Nova证明系统(2)
主要见斯坦福大学Wilson Nguyen、Dan Boneh和微软研究中心Srinath Setty 2023年论文《Revisiting the Nova Proof System on a Cycle of Curves》。
前序博客见:
基于cycle of curves的Nova证明系统(1)
5. IVC Proof进一步压缩
本文提出了…
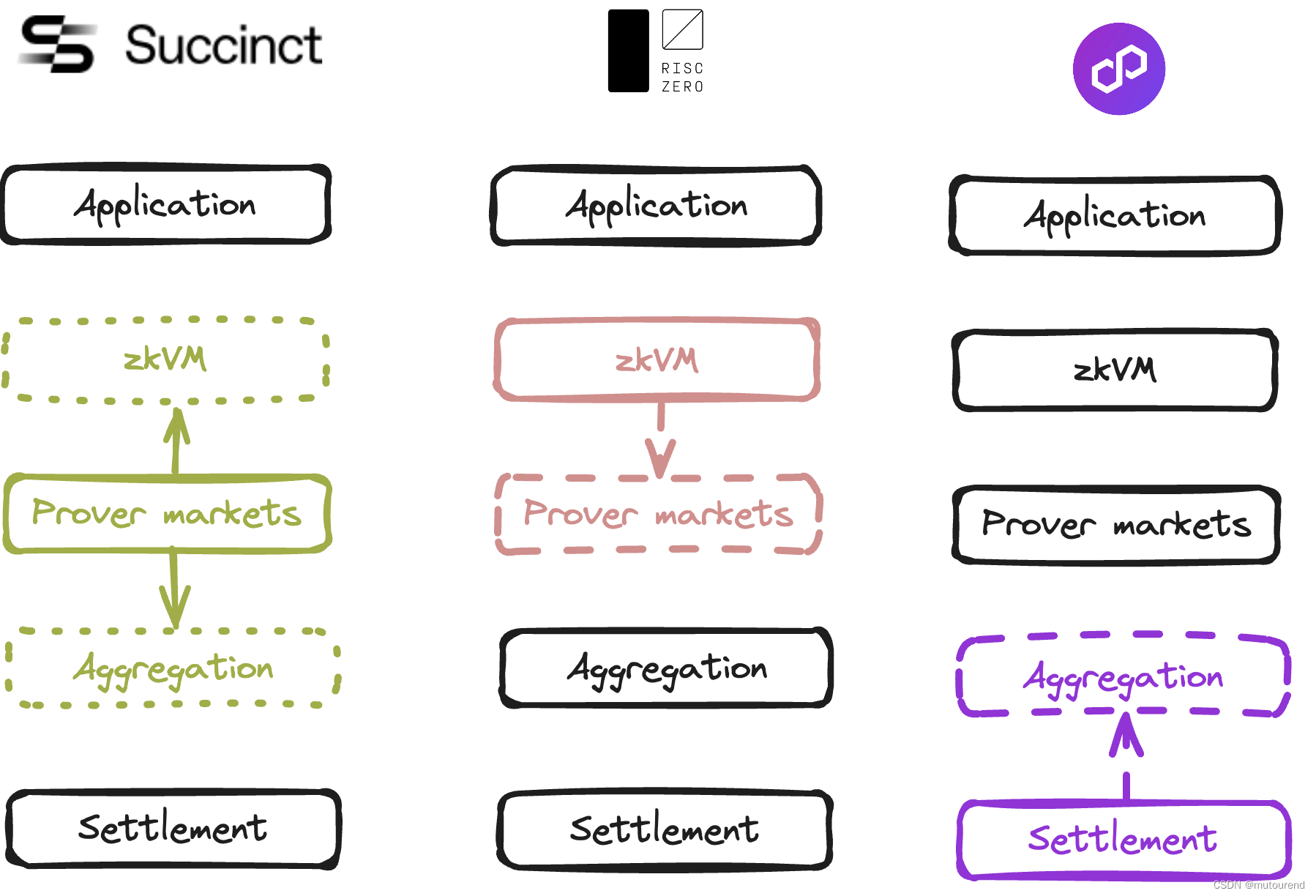
技术探秘:在RISC Zero中验证FHE——由隐藏到证明:FHE验证的ZK路径(1)
1. 引言
开源代码实现见:
https://github.com/hashcloak/fhe_risc0_zkvm(Rust)https://github.com/weikengchen/vfhe-profiled(Rust)https://github.com/l2iterative/vfhe0(Rust)
L2IV Resea…
ZK友好代数哈希函数安全倡议
1. 引言
前序博客:
ZKP中的哈希函数如何选择ZK-friendly 哈希函数?snark/stark-friendly hash函数Anemoi Permutation和Jive Compression模式:高效的ZK友好的哈希函数Tip5:针对Recursive STARK的哈希函数
随着Incrementally Ve…
高新技术企业到底有什么好处?
1、税收方面
企业的所得税率可以从认定前的25%降低至15%,税率降低10个点,税额减少40%。
2、对企业的品牌形象有所提升
通过高新技术企业认定后,说明企业是国家重点支持的具有高成长性的企业,具有较高的科技创新能力、较好的经济…
算术化电路中如何使用定制gates?
1. 引言
现有ZKP证明系统中,除关注proof size和verification time之外,Prover Time是一个重要瓶颈。 当侧重Prover Time时,可考虑STARK方案。并借助recursive STARKSNARK,来获得small proof。
Prover Time:
直接取…
零知识证明(zk-SNARK)- groth16(一)
全称为 Zero-Knowledge Succinct Non-Interactive Argument of Knowledge,简洁非交互式零知识证明,简洁性使得运行该协议时,即便 statement 非常大,它的 proof 大小也仅有几百个bytes,并且验证一个 proof 的时间可以达…
5+非肿瘤+WGCNA+PPI+实验,简单WGCNA分析思路,干湿结合
今天给同学们分享一篇非肿瘤WGCNAPPI的生信文章“Identification and Evaluation of Hub Long Noncoding RNAs and mRNAs in High Fat Diet Induced Liver Steatosis”,这篇文章于2023年2月14日发表在Nutrients期刊上,影响因子为5.9。 非酒精性脂肪肝病&…
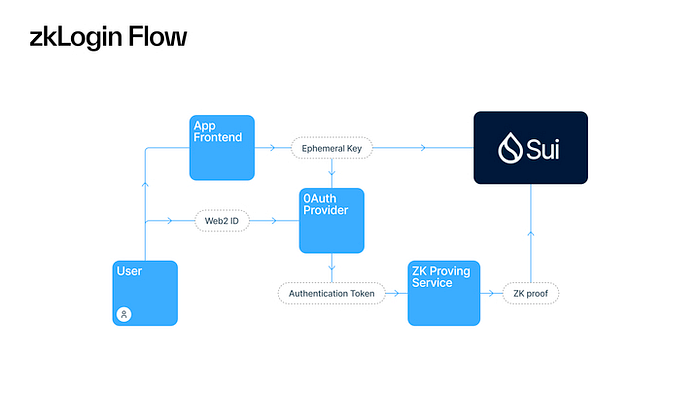
Sui账户抽象消除用户使用障碍,让大规模用户使用区块链成为可能
Sui通过其本机语言和两个特定功能实现了账户抽象,使账户管理中更加细节化的过程自动化。无论是zkLogin还是赞助交易,都简化了用户的使用过程,而Sui Move的基本结构则使开发人员能够提供丝滑的体验。
最近,随着区块链寻求扩大其用…
STARKs with small finite field:小域带来的迷人性能
1. 引言
前序博客有:
2023年 ZK Hack以及ZK Summit 亮点记为何需关注各ZKP方案的benchmarks?
很久以前,有大量研究和开发致力于改进ZKP性能。研究人员通过采用多种不同的技术,包括但不限于:
不同的IOPs不同的多项式…
7+非肿瘤+WGCNA+分型+实验,筛选关键基因进一步分型以及表达验证
今天给同学们分享一篇非肿瘤WGCNA分型实验的生信文章“Identification of molecular subtypes and immune infiltration in endometriosis: a novel bioinformatics analysis and In vitro validation”,这篇文章于2023年8月18日发表在Front Immunol期刊上ÿ…
GKR+Groth16:更快的MiMC证明
1. 引言
Consensys团队Alexandre Belling等人2022年论文 Recursion over Public-Coin Interactive Proof Systems; Faster Hash Verification 中,提出了:
用GKR来证明MiMC哈希计算的完整性将GKR verifier嵌入到SNARK(Groth16)电…
零知识证明的最新发展和应用
PrimiHub一款由密码学专家团队打造的开源隐私计算平台,专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。 当企业收集大量客户数据去审查、改进产品和服务以及将数据资产货币化时,他们容易受到网络攻击威胁,造成数…
3. ZKP 之 zksnark 协议实现
SNARKs的基本思路是 C o m p u t a t i o n → A r i t h m e t i c C i r c u i t →
1. ZKP 研究框架及相关内容概述
ZK简介
最初在1980年提出,由Shafi Goldwasser, Silvio Micali和Charles Rackoff。刚开始叫做交互式证明系统 (Interactive proof system)。
Prover 和 Verifier 之间交换信息,让 Verifier 相信某种 statement 是真的。而不透露给 Verifier 过多与证明无关的信息。
ZK 是解…
5+铁死亡+分型+WGCNA+机器学习分析
今天给同学们分享一篇铁死亡分型WGCNA机器学习的生信文章“Identification of ferroptosis-related molecular clusters and genes for diabetic osteoporosis based on the machine learning”,这篇文章于2023年8月14日发表在Front Endocrinol (Lausanne)期刊上&am…
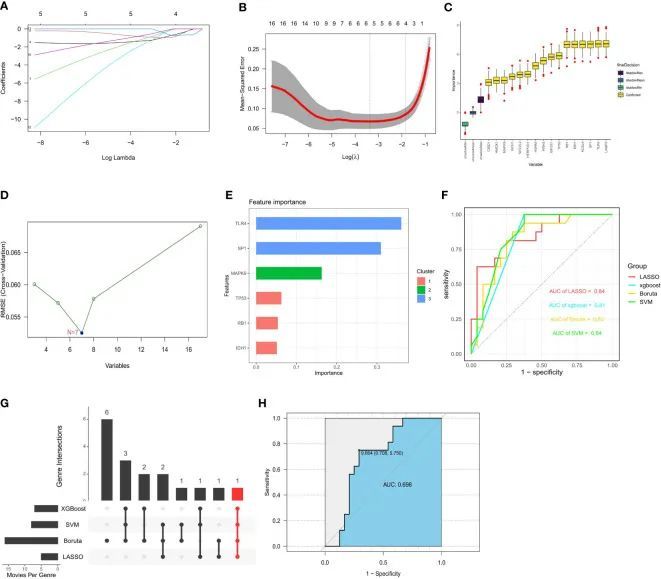
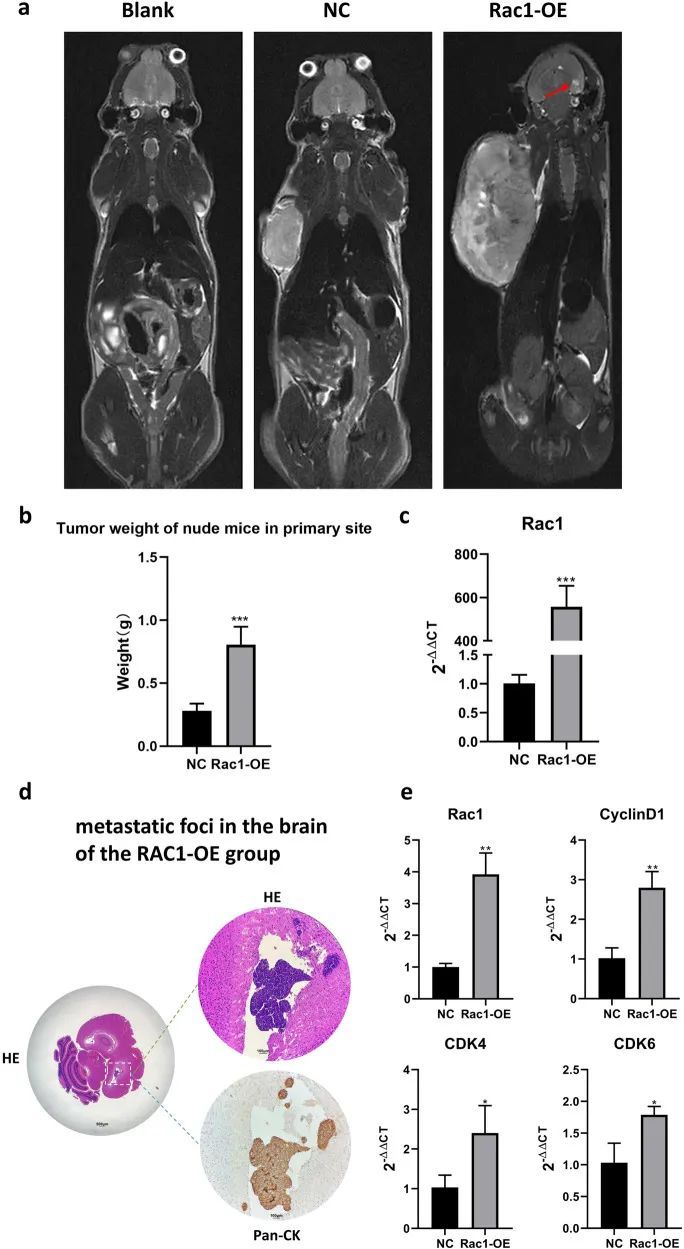
9+单细胞+实验验证,探讨单基因对癌细胞转移作用的思路方向
今天给同学们分享一篇单细胞实验的生信文章“Identification of RAC1 in promoting brain metastasis of lung adenocarcinoma using single-cell transcriptome sequencing”,这篇文章于2023年5月18日发表在Cell Death Dis期刊上,影响因子为9。 本研究旨…
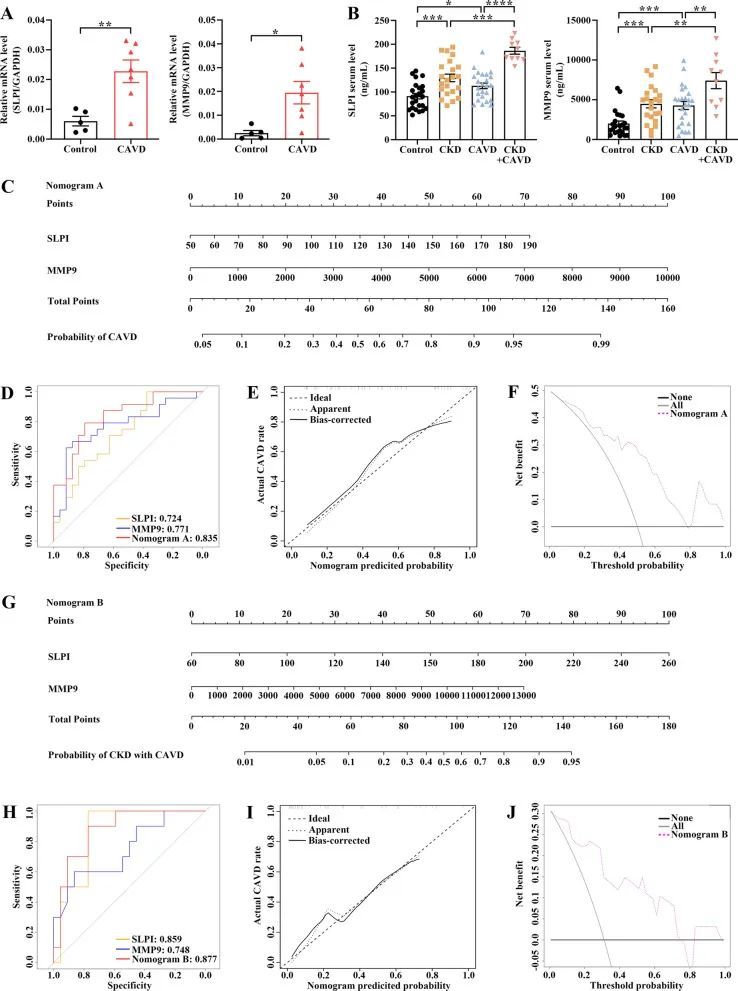
非肿瘤纯生信拿下7+,多种机器学习算法,搭配WGCNA。
今天给同学们分享一篇非肿瘤WGCNA机器学习的生信文章“Screening of immune-related secretory proteins linking chronic kidney disease with calcific aortic valve disease based on comprehensive bioinformatics analysis and machine learning”,这篇文章于2…
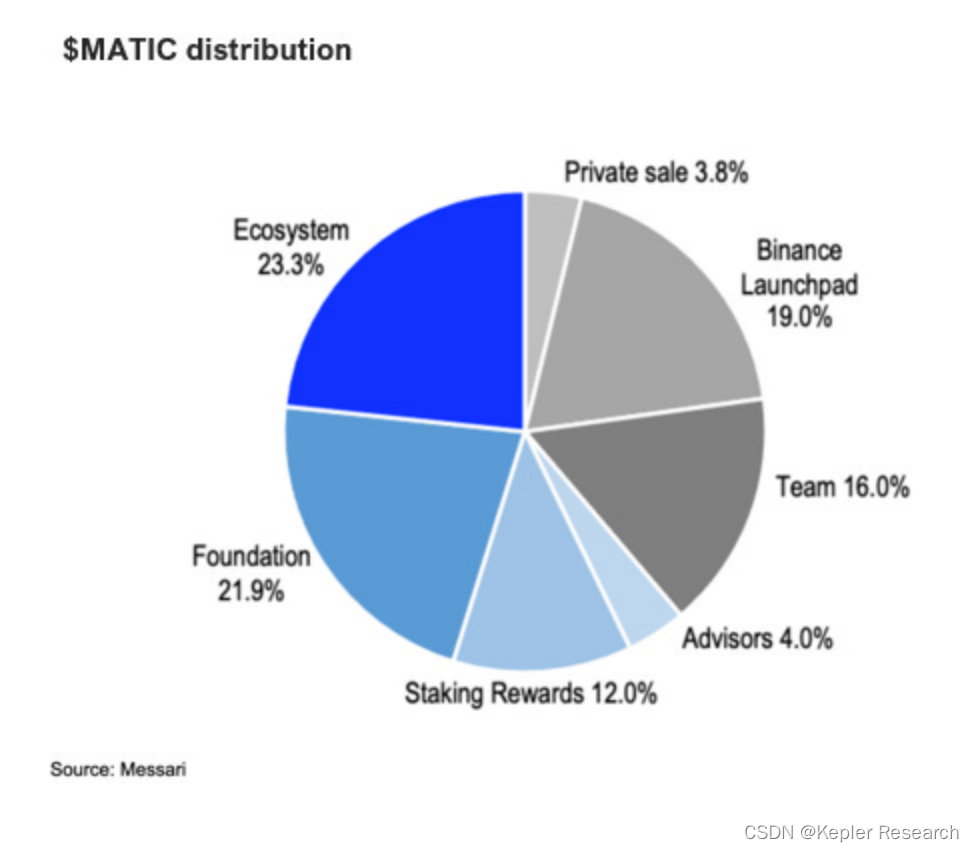
引领创新浪潮:“Polygon探寻新技术、新治理、新代币的未来之路!“
熊市是用来建设的,Polygon Labs一直在利用这漫长的几个月来做到这一点。
Polygon 是最常用的区块链之一,每周约有 150 万用户,每天超过 230 万笔交易,以及数千个 DApp,Polygon 最近面临着日益激烈的竞争。虽然从交易数…
比特币减半期望:“激发投资者热情,引爆下一个财富革命的期待“
为什么投资比特币?
首先比特币是最好的货币没有之一
"比特币与所有其他资产不同,因为它具有不可改变的稀缺性的独特属性。与其他商品不同,比特币具有预定的算法供应计划,无法更改。无论怎么修改,比特币永远不会…
9+铜死亡+缺氧+分型+单细胞+实验生信思路
今天给同学们分享一篇铜死亡缺氧分型实验的生信文章“Unraveling Colorectal Cancer and Pan-cancer Immune Heterogeneity and Synthetic Therapy Response Using Cuproptosis and Hypoxia Regulators by Multi-omic Analysis and Experimental Validation”,这篇文…
SNARK超详细解释,从GGPR13到Groth16
初学零知识证明,准备从SNARK开始入手,还是自己做个整理会印象深刻一些 目前看来GGPR13是最先提出基于QAP的SNARK这个框架的工作,而Groth16则是目前效率表现最好的SNARK方案。话说Craig Gentry大佬也太牛了吧,不止是全同态加密的鼻…
Binius:基于binary fields的SNARKs(Part 2)
1. 引言
前序博客有:
Binius:基于binary fields的SNARKs(Part 1)Binius:助力ZK行业发展
本文重点关注:
1)concatenated codes:可扩展对small fields的多项式承诺方案2࿰…
Sui安全篇|详解零知识证明 (ZKP) Groth16的可塑性
Sui Move允许用户使用Groth16进行高效验证任何非确定性多项式时间(Non-deterministic Polynomial time ,NP)状态。Groth16是一种高效且广泛使用的零知识简洁非交互知识证明(Zero-Knowledge Succinct Non-interactive Argument of …
PLONK 的工作原理:第 2 部分
在第 1 部分中,我们解释了如何将想要使用 PLONK 证明的计算转换为中间约束系统,最终使用多项式承诺方案 (PCS) 来证明。我们只介绍了一种类型的约束:门约束。在本文中,我们将介绍另一种类型:复制约束。
复制约束 图 1…
ZKP5.2 PLONK IOP
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 5: The Plonk SNARK (Dan Boneh)
5.2 Proving properties of committed polynomials overview Polynomial equality testing with KZG KZG: determined commitment (if the function is equal, then the commitment is equa…
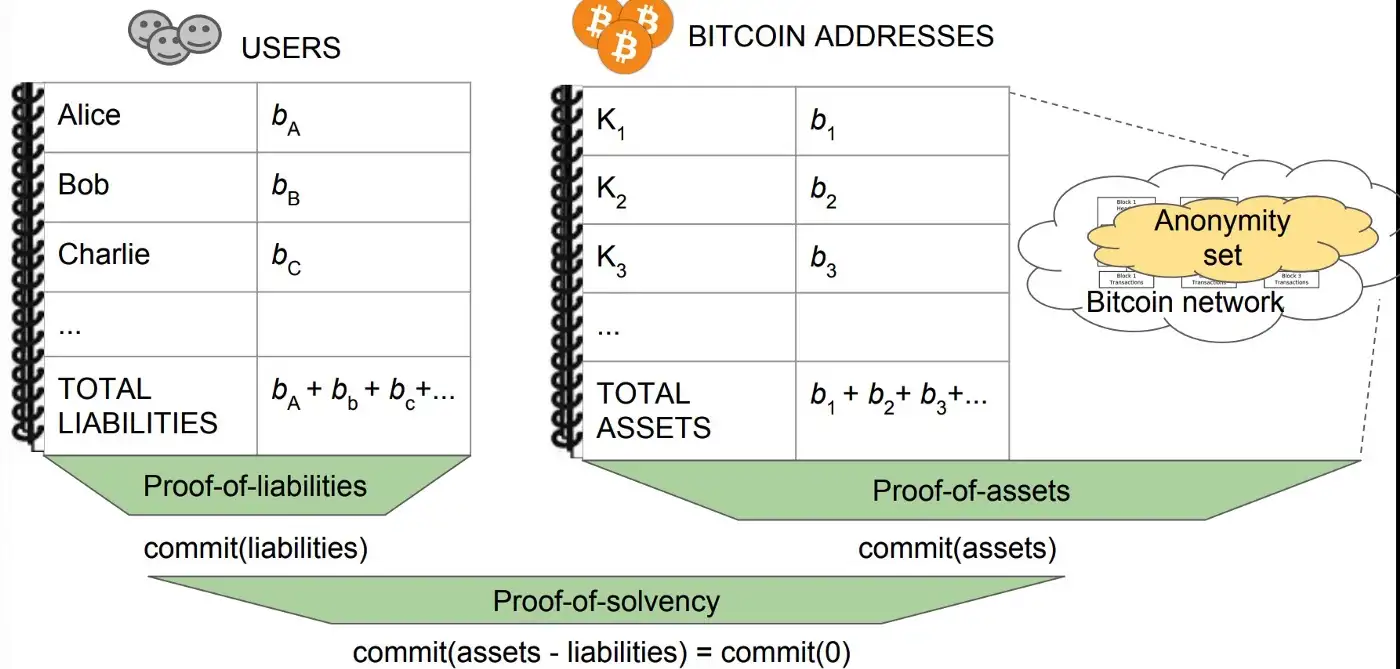
加密货币交易所偿付能力的零知识证明
如何检测下一个 FTX 和 Mt. Gox 加密货币交易所 FTX 的内爆导致数十亿客户资金流失,这是加密货币历史上交易所破产的最新例子。历史可以追溯到 2014 年,当时处理 70% 比特币交易的历史最悠久、规模最大的交易所 Mt. Gox 丢失了用户的 850,000 个比特币。…
零知识证明友好的波塞冬哈希(ZK-friendly Hashing: Poseidon)
文章目录 背景什么是 Poseidon 哈希技术原理各STARK friendly hash函数性能对比SHA256 VS Pedersen参考背景
2018年7月2日,以太坊基金会给StarkWare团队2年的赞助,用于寻找新的STARK friendly hash (SFH) 函数,可用于在区块链中构建transparent且抗量子安全的proof系统。
…
基于Towers of Binary Fields的succinct arguments
1. 引言
Ulvetanna团队Benjamin E. Diamond和Jim Posen 2023年论文《Succinct Arguments over Towers of Binary Fields》,开源代码见:
https://github.com/recmo/binius(Rust Sage)【基于plonky3等库】
在该论文中࿱…
2023 年和 2024 年 10 个最佳加密货币趋势
1.熊市低迷
加密货币市场已进入持续数月的长期看跌阶段。尽管 2023 年初出现了一些看涨走势,但大多数领先的加密货币随后都出现了看跌低迷,导致其市值大幅下跌。
此外,持续的熊市可归因于一系列因素,包括宏观经济不确定性、利率…
Solidity案例详解(四)投票智能合约
该合约为原创合约,功能要求如下 在⼀定时间能进⾏投票超过时间投票截⽌,并投赞同票超过50%则为通过。 使⽤safeMath库,使⽤Owner 第三⽅库拥有参与投票权的⽤户在创建合约时确定Voter 结构 要有时间戳、投票是否同意等;struct 结构…
Sui Lutris:Sui核心的分布式系统协议
经过数个月的测试,Mysten Labs于 8月18日更新了Sui Lutris白皮书,确定了以下内容:
使用PTBs和5K TPS,Sui每秒可以处理140k至150k次操作,这表明Sui在主网峰值(约700 TPS)下的基准测试远低于其实…
深入探索STARK的安全性和可靠性——STARKs全面安全分析
1. 引言
non-interactive STARKs,起源于Interactive Oracle Proofs (IOPs),然后通过random oracle模式转换为非交互式。StarkWare团队 ethSTARK Documentation – Version 1.2(2023年7月)论文做了更新,给出了完整具体…
ZKP15.3 Formal Methods in ZK (Part II)
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 15: Secure ZK Circuits via Formal Methods (Guest Lecturer: Yu Feng (UCSB & Veridise))
15.3 Formal Methods in ZK (Part II) Formally prove that a circuit is NOT underconstrained Existing Strategies Static …
Plonky2:最好的SNARKs和STARKs
1. 引言 Plonky2为Polygon团队2022年1月发起的项目。其定位为ZKP证明系统。 开源代码实现见:
https://github.com/0xPolygonZero/plonky2(Rust 汇编)
Plonky2可解锁当今2大主流ZKP类型——SNARKs和STARKs的扩容优势。
每个ZKP证明系统都有…
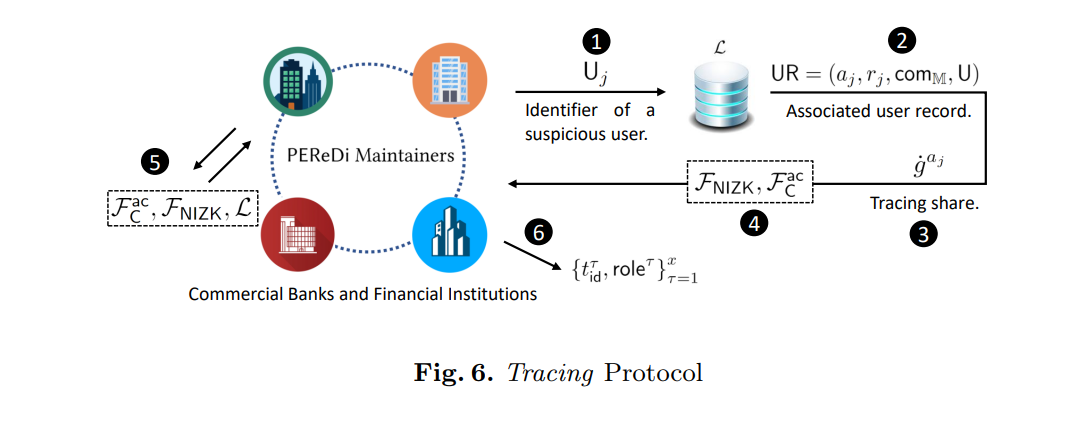
PEReDi 完全隐私的央行数字货币方案
第一个对完全隐私保护建模的方案,基于账户模型,要求交易双方都在线。
角色分类
中央银行 B B B:负责发行数字货币和货币政策,但不控制用户账户的状态,没有能力对交易的发送者或接收者进行去匿名化或披露与特定交易相…
zk-Bench:SNARKs性能对比评估工具
1. 引言
JENS ERNSTBERGER等人2023年论文《zk-Bench: A Toolset for Comparative Evaluation and Performance Benchmarking of SNARKs》。
zk-Bench,定位为:
定位为首个公钥密码学性能评估基准测试框架和工具,重点关注通用ZKP系统的实测评…
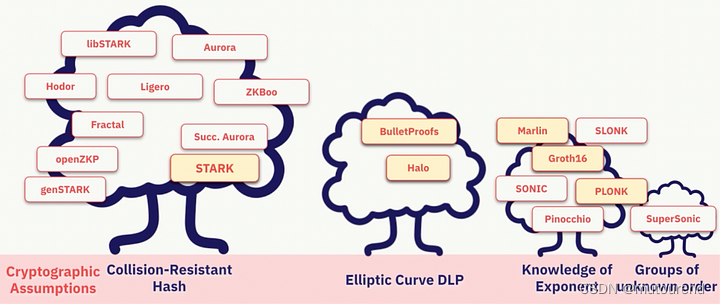
密码学证明方案寒武纪大爆发——扩容、透明性和隐私的变革潜力
1. 引言
前序博客有:
ZKP大爆炸
本文主要参考:
StarkWare 2023年6月博客 Cambrian Explosion of Cryptographic Proofs----The transformative potential for scalability, transparency, and privacy2023年3月Eli Ben-Sasson在The 13th BIU Winter …
押注零知识证明赛道,Conflux与ACCSEAL达成战略合作
Conflux与新兴零知识证明加速芯片制造公司ACCSEAL宣布达成战略合作,携手共同布局零知识证明(Zero-Knowledge Proof,简称ZKP)赛道,探索可应用于Conflux生态系统的最先进零知识证明技术和解决方案。早在2022年3月&#x…
ZKP Mathematical Building Blocks 1
MIT IAP 2023 Modern Zero Knowledge Cryptography课程笔记
Lecture 3: Mathematical Building Blocks (Yufei Zhao) Example: I (Prover) want to convince you (Verifier) that I can distinguish two colors that you see as identical A Similar Example: How to prove t…
零知识证明(zk-SNARK)(一)
全称为 Zero-Knowledge Succinct Non-Interactive Argument of Knowledge,简洁非交互式零知识证明,简洁性使得运行该协议时,即便statement非常大,它的proof大小也仅有几百个bytes,并且验证一个proof的时间可以达到毫秒…
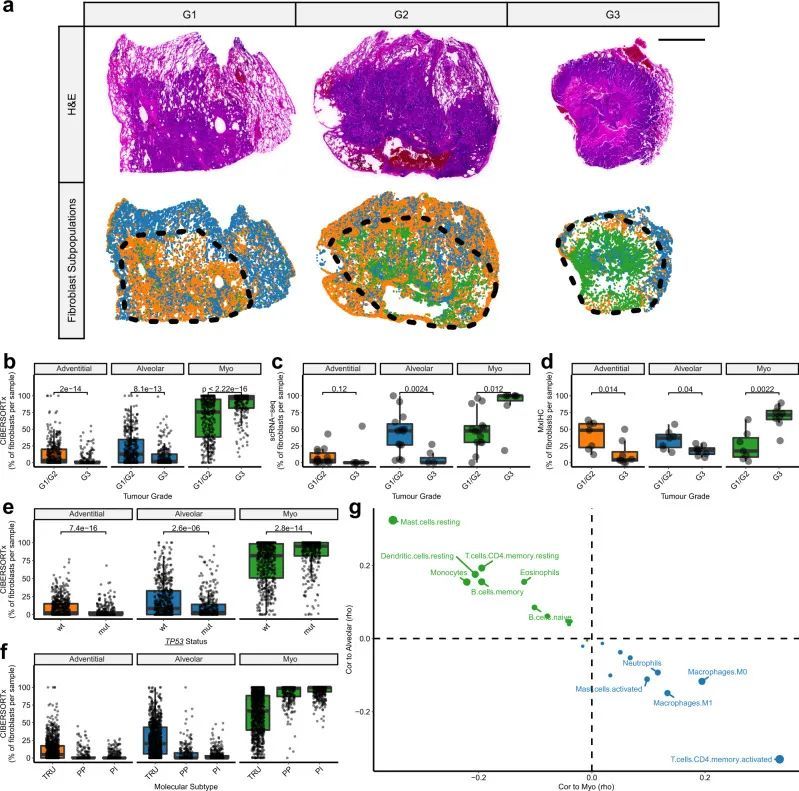
16+sci,多重免疫组织化学+CIBERSORTx 鉴定成纤维细胞亚群。
今天给同学们分享一篇单细胞多重免疫组织化学数字细胞学(CIBERSORTx)的生信文章“Single-cell analysis reveals prognostic fibroblast subpopulations linked to molecular and immunological subtypes of lung cancer”,这篇文章于2023年1…
ZKP7.3 Linear-time encodable code based on expanders
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 7: Polynomial Commitments Based on Error-correcting Codes (Yupeng Zhang)
7.3 Linear-time encodable code based on expanders SNARKs with linear prover time Linear-time encodable code [Spielman’96][Druk-Ishai…
压箱底的企业知识管理软件来啦,赶紧收藏!
在这个知识经济日益突出的时代,企业对知识管理的需求前所未有的大。一个优秀的知识管理软件,仿佛企业的大脑,能够高效地连接信息,促进知识的传播和利用。今天,我们就为大家一口气推荐三款齐声赞誉的企业知识管理软件&a…
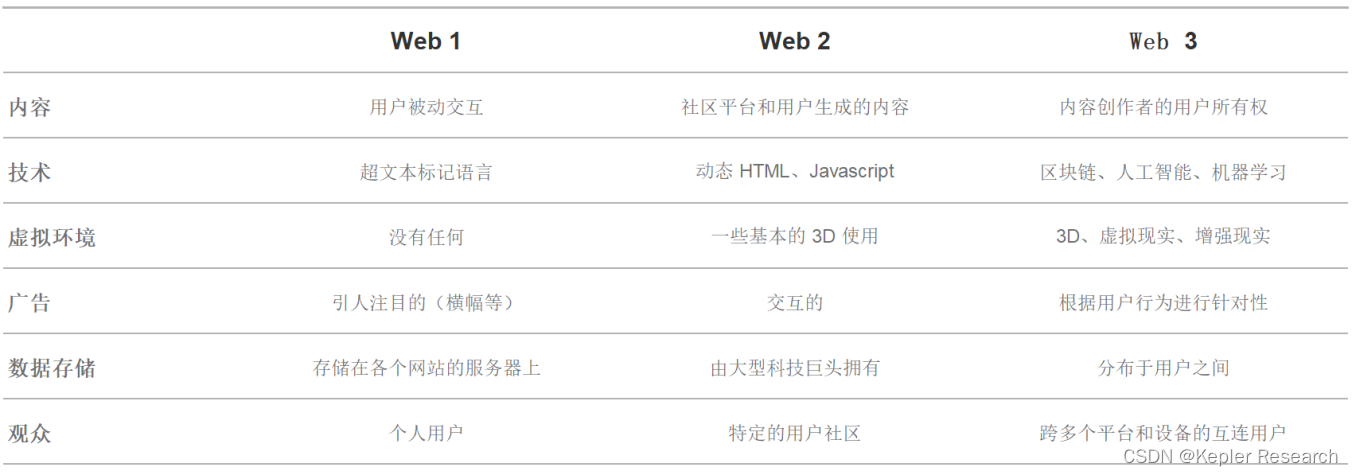
“Web 3.0引领未来:下一代互联网技术将来袭!“
"下一代互联网技术,称为Web 3.0或Web3,主要利用机器学习、人工智能(AI)和区块链技术。" 与 Web2 相比,Web3 为消费者提供了对其在线数据的更多自主权,而Web2 专注于托管在”集中式“网站上的用户…
ZKP Understanding Nova (2) Relaxed R1CS
Understanding Nova
Kothapalli, Abhiram, Srinath Setty, and Ioanna Tzialla. “Nova: Recursive zero-knowledge arguments from folding schemes.” Annual International Cryptology Conference. Cham: Springer Nature Switzerland, 2022.
Nova: Paper Code
2. Unders…
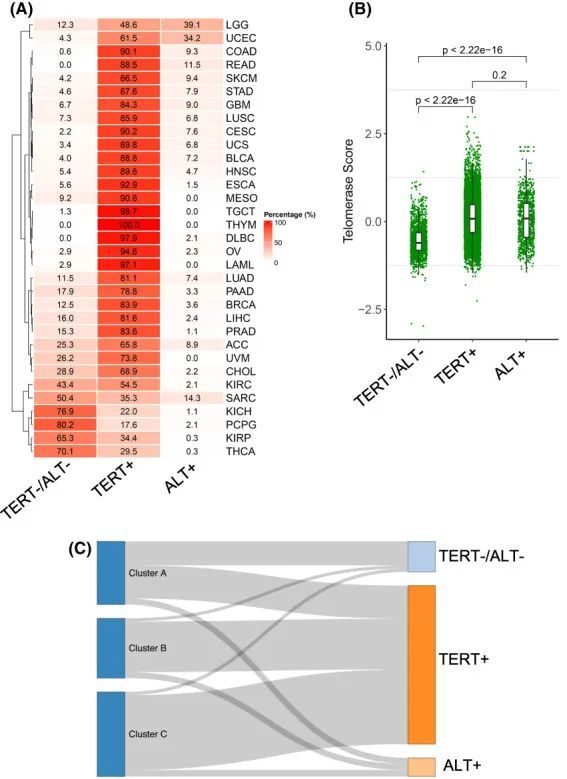
端粒/端粒酶生信切入点,6+端粒酶+泛癌+甲基化+实验。
今天给同学们分享一篇端粒酶泛癌甲基化实验的生信文章“Genomic, epigenomic, and transcriptomic signatures for telomerase complex components: a pan‐cancer analysis”,这篇文章于2022年10月31日发表在Mol Oncol期刊上,影响因子为6.6。 激活端粒酶…
专访 Hyper Oracle:可编程的 zkOracle 打造未来世界的超算
许多 Web3 应用在实现的过程中,常常会遇到基础设施方面的限制,包括去中心化自动化、预言机、链上信息搜索等问题。绝大部分区块链的中间件网络都是依赖于节点质押来保证节点执行的诚实性,这样的模式会产生诸多衍生问题,例如安全性…
FHEW 和 TFHE 的统一框架:标准化 FHE
参考文献:
[GHS12] Gentry C, Halevi S, Smart N P. Better bootstrapping in fully homomorphic encryption[C]//International Workshop on Public Key Cryptography. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 1-16.[GHPS12] Gentry C, Halevi S,…
5+非肿瘤分析,分型+WGCNA+机器学习筛选相关基因
今天给同学们分享一篇非肿瘤分型机器学习WGCNA实验的生信文章“Identification of diagnostic markers related to oxidative stress and inflammatory response in diabetic kidney disease by machine learning algorithms: Evidence from human transcriptomic data and mou…
BabySpartan:对non-uniform computation的Lasso-based SNARK
1. 引言
前序博客有:
Lasso、Jolt 以及 Lookup Singularity——Part 1Lasso、Jolt 以及 Lookup Singularity——Part 2深入了解LassoJoltmultilinear多项式承诺方案benchmark对比
见Srinath Setty和Justin Thaler 2023年论文《BabySpartan: Lasso-based SNARK fo…
ZKP11.4 Use CI to instantiate Fiat-Shamir
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 11: From Practice to Theory (Guest Lecturer: Alex Lombardi)
11.4 Use CI to instantiate Fiat-Shamir Avoid Bad Challenges Def: Given false claim x x x and a first message α \alpha α, a challenge β \beta …
零知识证明的应用场景-1用户登录
零知识证明(Zero-Knowledge Proof, ZKP)是一种密码学方法,它允许一方向另一方证明某个陈述的真实性,而不会泄露任何有关该陈述的其他信息。这种技术在许多场景中都非常有用,尤其是在需要保护隐私的场合。
在身份验证的…
8+单基因+细胞凋亡+WGCNA+单细胞+实验验证
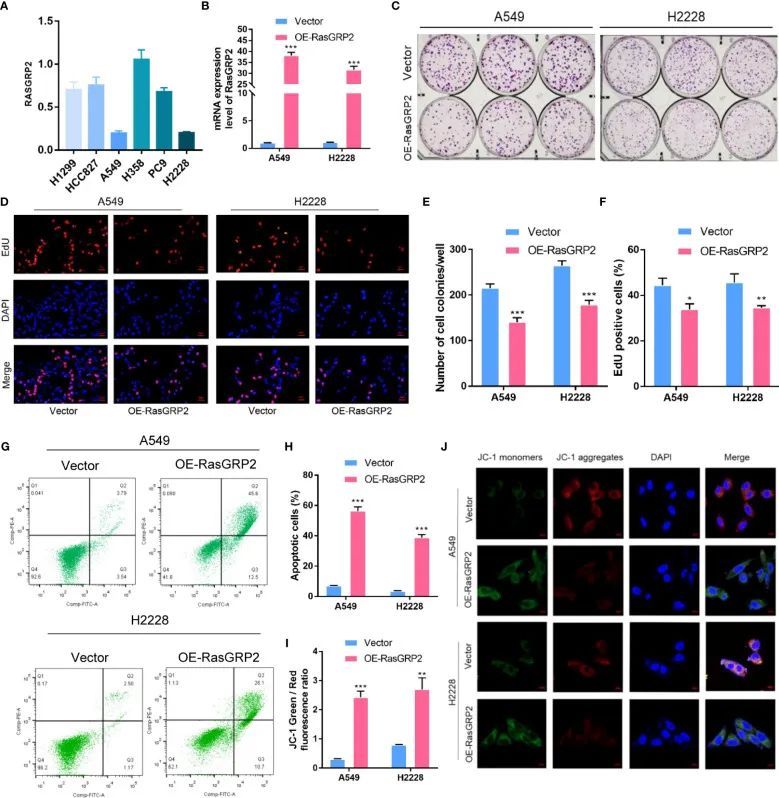
今天给同学们分享一篇单基因细胞凋亡WGCNA实验验证的生信文章“RASGRP2 is a potential immune-related biomarker and regulates mitochondrial-dependent apoptosis in lung adenocarcinoma”,这篇文章于2023年2月3日发表在Front Immunol期刊上,影响因…
强势得分套路之一:单基因泛癌+实验验证
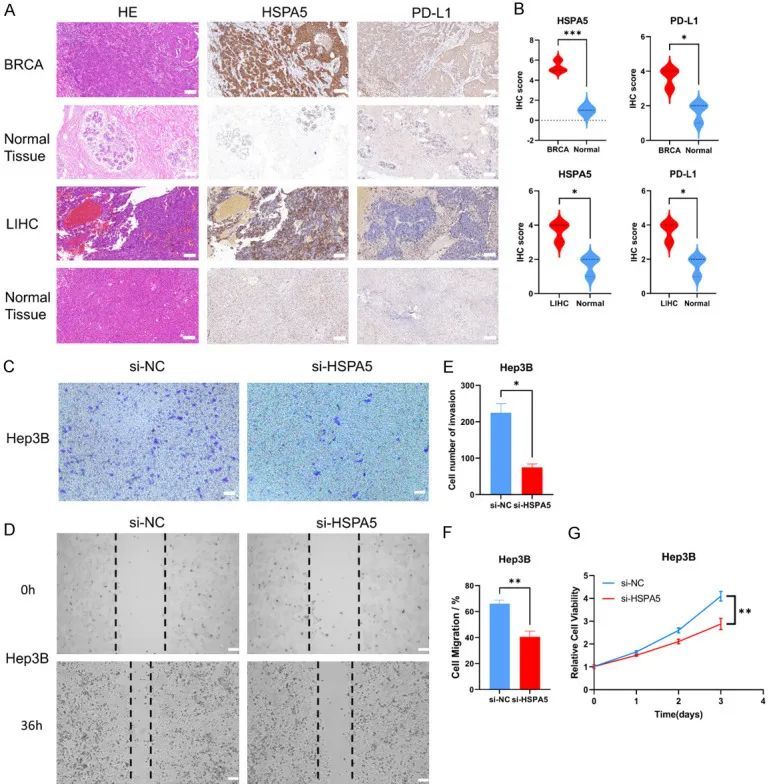
今天给同学们分享一篇单基因泛癌实验验证的生信文章“A human pan-cancer system analysis of heat shock protein family A member 5”,这篇文章于2023年5月15日发表在Am J Cancer Res期刊上,影响因子为5.2。 热休克蛋白家族A成员5(HSPA5&am…
MoveFunsDAO 星航计划|从Move入门Web3与深入实践「公益课堂」
Move 语言作为最安全的编程语言之一,在资产的安全性和保护方面有着显著优势,被寄予引领 Web3 世界的全新叙事的厚望。
随着 Sui 在今年五月主网上线,它为 Move 生态带来一股新的浪潮。上线以来,Sui 公链的开发活跃度持续数月位居…
技术探秘:在RISC Zero中验证FHE——RISC Zero应用的DevOps(2)
1. 引言
前序博客:
技术探秘:在RISC Zero中验证FHE——由隐藏到证明:FHE验证的ZK路径(1)
技术探秘:在RISC Zero中验证FHE——由隐藏到证明:FHE验证的ZK路径(1) 中&…
基于KZG多项式承诺方案的RLN
1. 引言
RLN——Rate-Limiting Nullifier为PSE团队主导的项目,源自:
Barry White Hat 2019年博客 Semaphore RLN, rate limiting nullifier for spam prevention in anonymous p2p setting
RLN(Rate-Limiting Nullifier)是一种…
Polygon zkEVM中的Recursive STARKs
1. 引言
主要参看Polygon zkEVM创始人Jordi在2023年StarkWare Sessions上的分享:
StarkWare Sessions 23 | Recursive STARKs in the zkEVM Context | Jordi Baylina
整个Polygon zkEVM circuit为一个巨大的STARK circuit。 Polygon zkEVM目前采用的递归聚合方案…
5+预后模型+实验验证
今天给同学们分享一篇SUMO化修饰预后模型实验验证的生信文章“The Prognosis-Predictive and Immunoregulatory Role of SUMOylation Related Genes: Potential Novel Targets in Prostate Cancer Treatment”,这篇文章于2023年9月2日发表在Int J Mol Sci期刊上&…
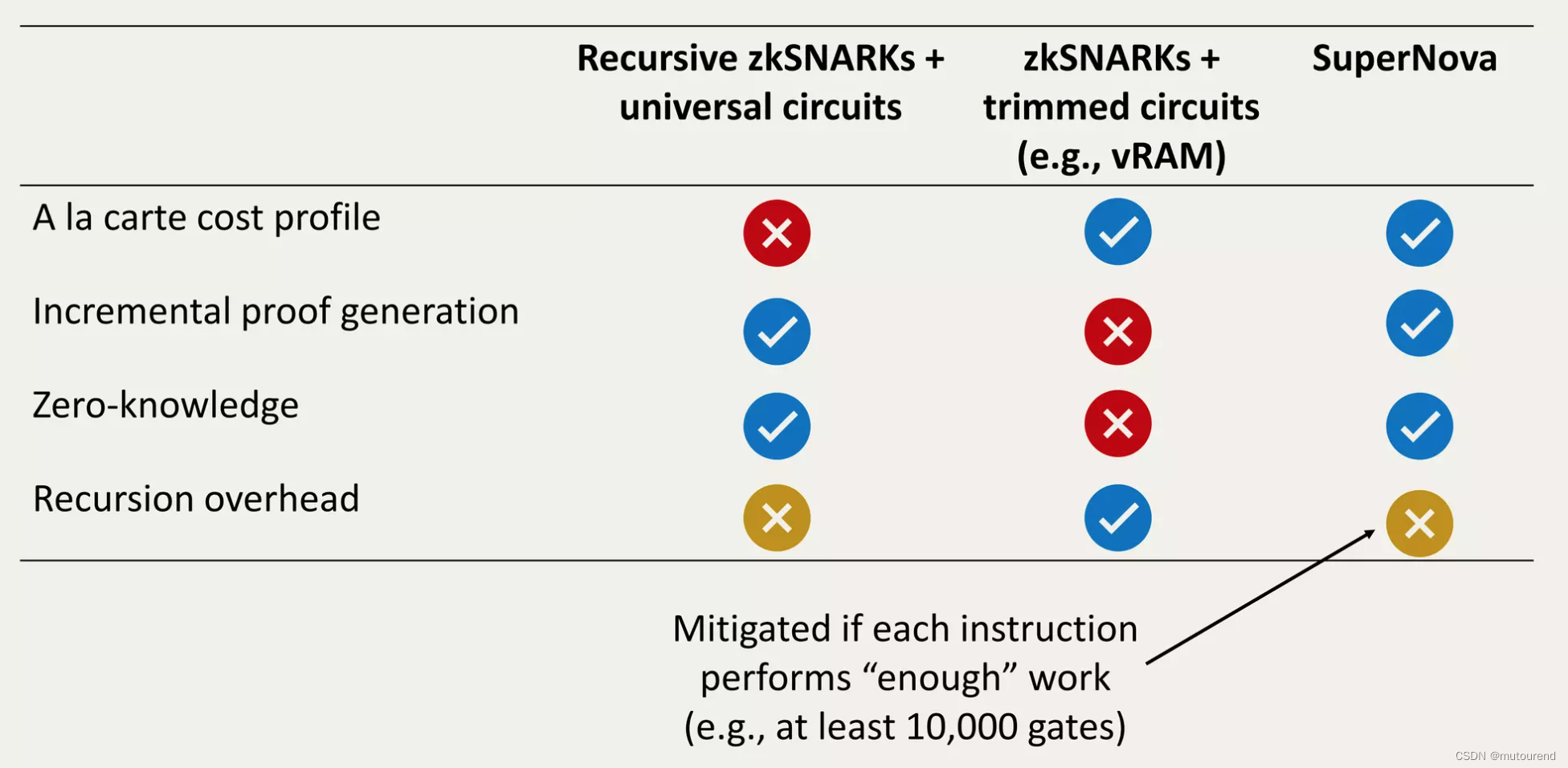
Nova 和 SuperNova:无需通用电路的通用机器执行证明系统
1. 引言
前序博客有:
Nova: Recursive Zero-Knowledge Arguments from Folding Schemes学习笔记SuperNova:为多指令虚拟机执行提供递归证明基于Nova/SuperNova的zkVMSangria:PLONK Folding2023年 ZK Hack以及ZK Summit 亮点记Sangria&…
Impagliazzo five-worlds
参考文献:
Impagliazzo R. A personal view of average-case complexity[C]//Proceedings of Structure in Complexity Theory. Tenth Annual IEEE Conference. IEEE, 1995: 134-147. 文章目录 五个世界AlgorithmicaHeuristicaPessilandMinicryptCryptomania 五个世…
欧洲大学专场黑客松,获奖者们在Sui上构建链上物品验证并改进荷兰拍卖
在由区块链学生协会(Blockchain Student Association)与Sui合作的黑客松上,获奖者们构建了旨在吸引新用户并弥合区块链技术与实物资产之间差距的项目。这些新项目展示了Sui的发展前景和灵活性,以及它如何解决现实世界的问题。
来…
“比特币市场风起云涌:第三季度报告揭示表现和未来趋势“
要点: 比特币的季度价格表现较差,为 -11.5%,但今年迄今为止的表现仍优于大多数资产类别; 截至撰写本文时,上半年推动比特币上涨的美国购买力已完全减弱; 交易量、流动性、波动性和搜索趋势均继续…
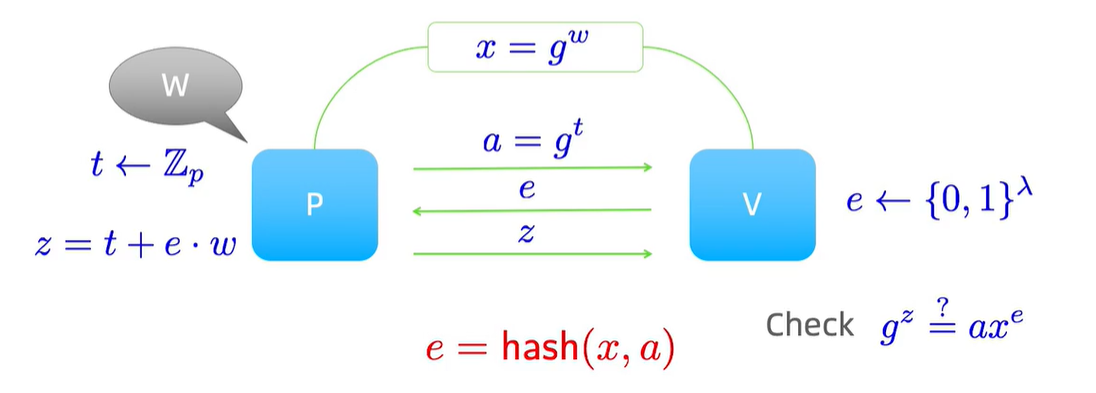
零知识证明(Sigma和Flat-shamir)
概述
定义:大概的定义就是prover可以向verifier证明自己给定的信息是大概率正确的,但是不泄露任何附加信息,包含信息本身。 举例 这里以一个比较经典的例子,即向红绿色盲(无法区分红色和绿色,看红色和绿色…
ZKP5.1 Plonk Interactive Oracle Proofs (KZG‘10)
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 5: The Plonk SNARK (Dan Boneh)
5.1 KZG’10 general SNARK A polynomial commitment scheme A polynomial interactive oracle proof (IOP) Review: polynomial commitments The KZG poly-commit scheme commit a bind…
零知识证明(zk-SNARK)- groth16(二)
From Computational Problem to zk-SNARK
本部分就是将计算难题转换为多项式,然后使用zk-SNARK。(注:以下用 P,V 替代 Prover,Verifier)
计算难题->R1CS
R1CS(Rank-1 Constraint System)是一种能够将…
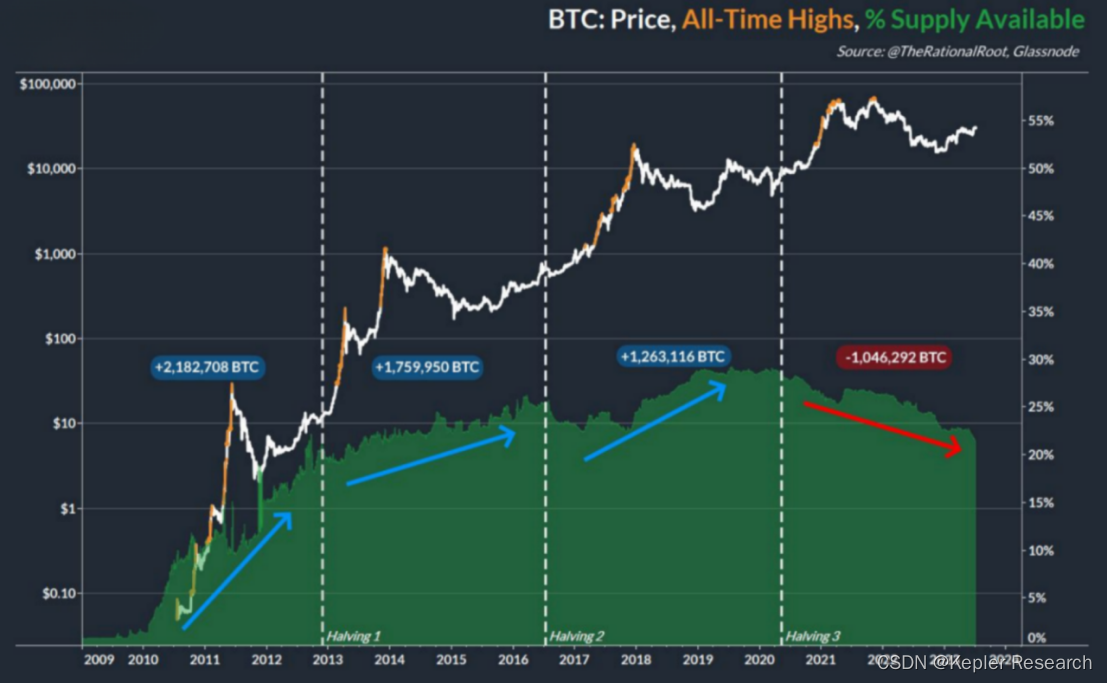
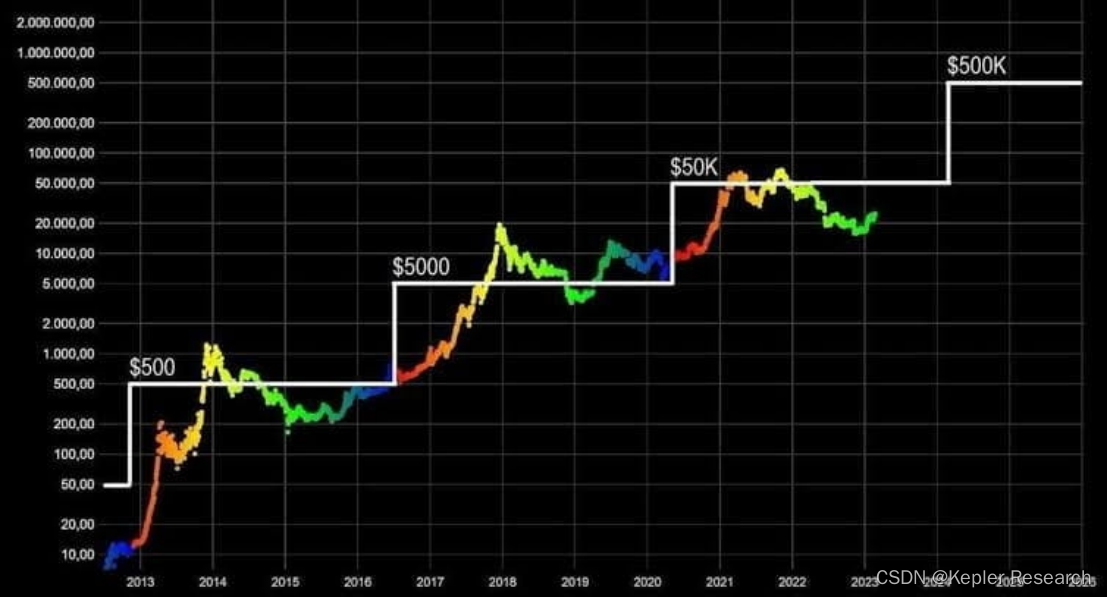
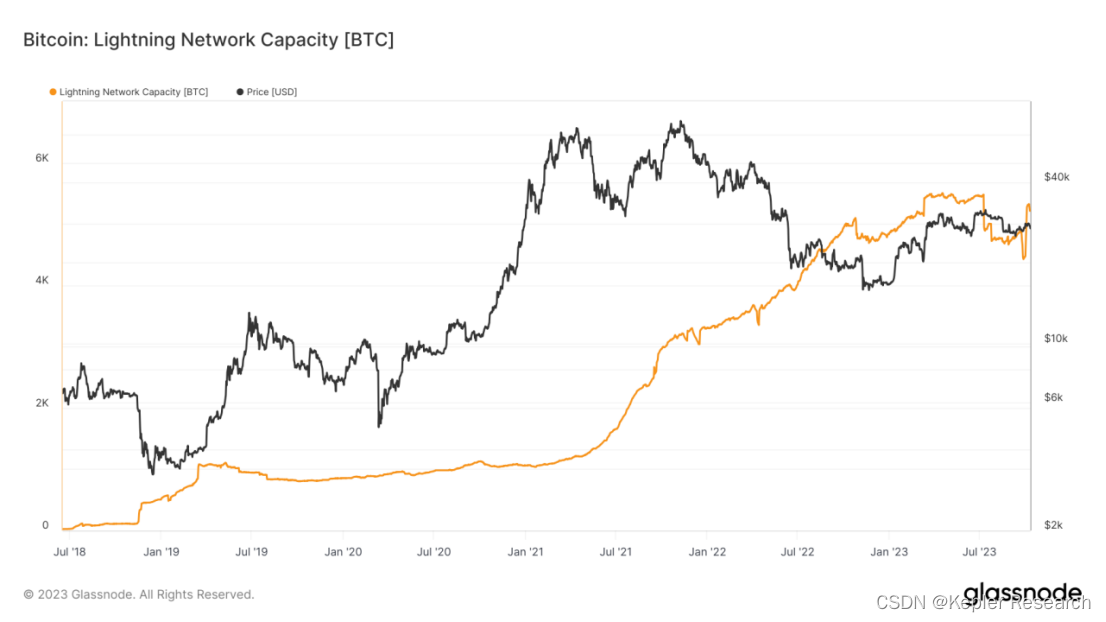
[2024区块链开发入门指引] - 比特币运行原理
一份为小白用户准备的免费区块链基础教程 工欲善其事,必先利其器
Web3开发中,各种工具、教程、社区、语言框架.。。。 种类繁多,是否有一个包罗万象的工具专注与Web3开发和相关资讯能毕其功于一役?
参见另一篇博文👉 2024最全面…
ZKP7.1 Polynomial Commitments Based on Error-correcting Codes (Background)
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 7: Polynomial Commitments Based on Error-correcting Codes (Yupeng Zhang)
Recall: common paradigm for efficient SNARK A polynomial commitment scheme A polynomial interactive oracle proof (IOP) SNARK for gene…
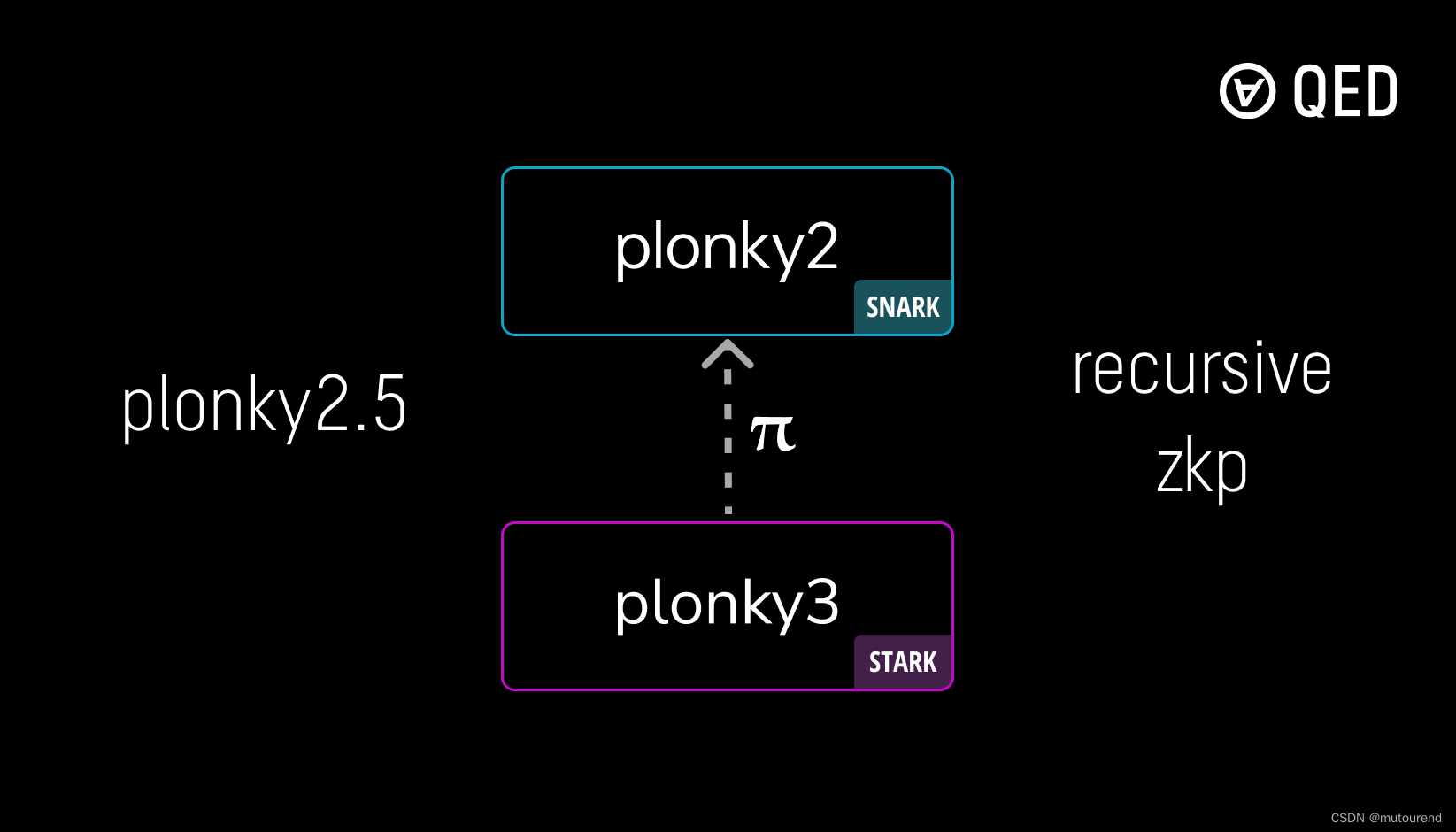
Plonky2.5:在Plonky2中验证Plonky3 proof
1. 引言 Plonky2.5为QED Protocol团队主导的项目,定位为:
在Plonky2 SNARK中验证Plonky3 STARK proof。
从而实现Plonky系列的递归证明。 开源代码实现见:
https://github.com/QEDProtocol/plonky2.5https://github.com/Plonky3/Plonky3&a…
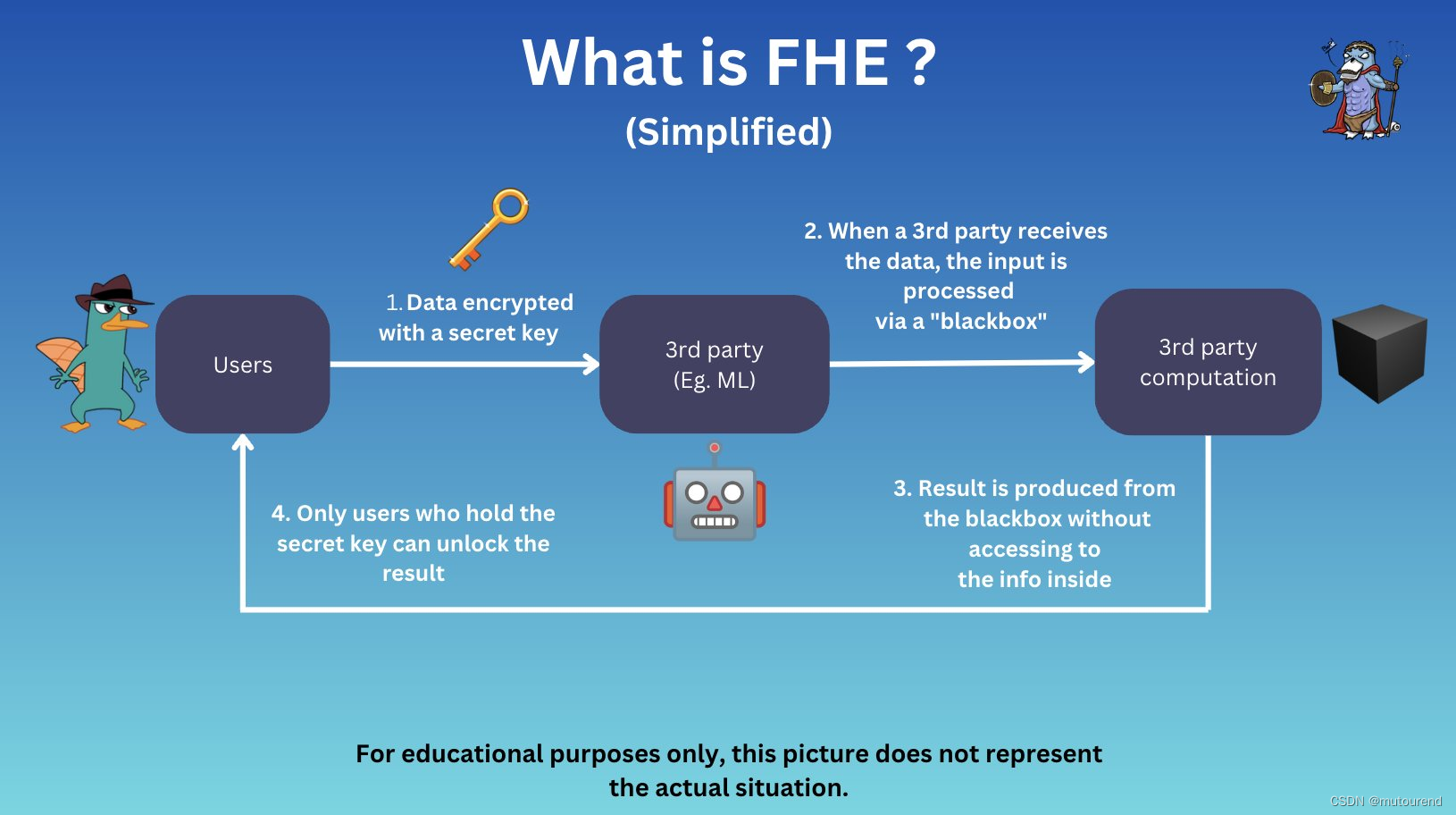
FHE全同态加密简介
1. 何为FHE? FHE (Fully homomorphic encryption):
是一种隐私技术,支持直接对密文进行计算,而无需对密文先解密再计算。即,任何第三方或云厂商,都可对敏感信息的密文进行处理,而无需访问密文内…
“地缘危机---通货紧缩风暴来袭,陷入深度困境!“
关于影响通胀动态的因素,我真正关注的是四个主要组成部分: 供应链 商品价格 工资 信用创造
“这些因素使我在2021年和2022年的通胀上升趋势以及2023年的下降趋势中保持正确的立场,因此我继续依赖它们作为未来通胀可能如何演变的指标。 ” …
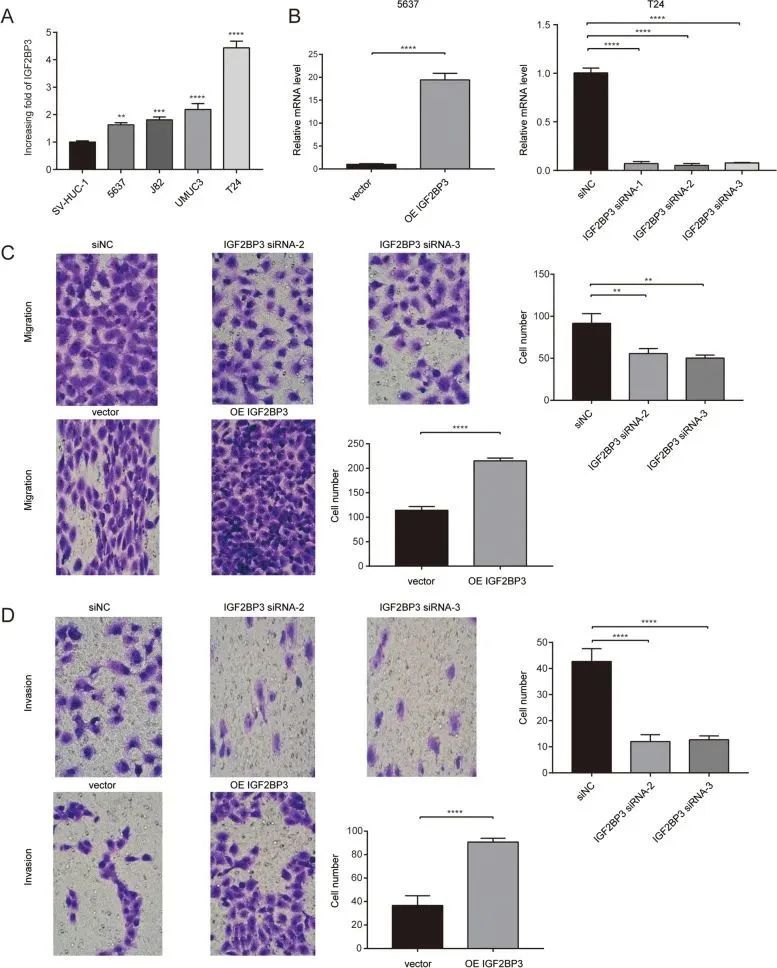
铜死亡+机器学习+WGCNA+分型生信思路
今天给同学们分享一篇单基因泛癌免疫实验生信文章“IGF2BP3 overexpression predicts poor prognosis and correlates with immune infiltration in bladder cancer”,这篇文章于2023年2月3日发表在BMC Cancer期刊上,影响因子为3.8。 膀胱癌是全球最常见…
3.6+铁死亡+WGCNA+机器学习
今天给同学们分享一篇3.6铁死亡WGCNA机器学习的生信文章“Identification of ferroptosis related biomarkers and immune infiltration in Parkinsons disease by integrated bioinformatic analysis”,这篇文章于2023年3月14日发表在BMC Med Genomics期刊上&#…
Sui基金会宣布将从外部做市商处收回1.17亿枚SUI,以支持生态和社区发展
Sui网络是一条突破性的L1区块链,于今年5月推出主网,并因可扩展性和行业领先的吞吐量而备受赞誉,被誉为最出色的区块链网络之一。由于这些$SUI之前已经释放,它们的重新分配不会影响$SUI的流通供应。这些$SUI还包括近日宣布的为Sui流…
ZKP11.3 Correlation Intractability
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 11: From Practice to Theory (Guest Lecturer: Alex Lombardi)
11.3 What can we do without random oracle model
Falsifiable Assumptions Prove security assuming that some concrete algorithmic task is infeasible: …
2023海内外零知识证明学习资料汇总(一)(故事中的零知识证明篇)
工欲善其事,必先利其器
Web3开发中,各种工具、教程、社区、语言框架.。。。 种类繁多,是否有一个包罗万象的工具专注与Web3开发和相关资讯能毕其功于一役?
参见另一篇博文👉 2024最全面且有知识深度的web3开发工具、web3学习项目…
PLONK电路如何构造,PLONK例子
文章目录个人总结如何理解电路Gate ConstraintsCopy constraints多项式承诺参考资料个人总结
PlonK相比起之前的zkSNARK协议来说,主要区别在于三点,
1-首先是在将电路解释为多项式的时候,SNARK协议一般采用R1CS到QAP的做法,最后…
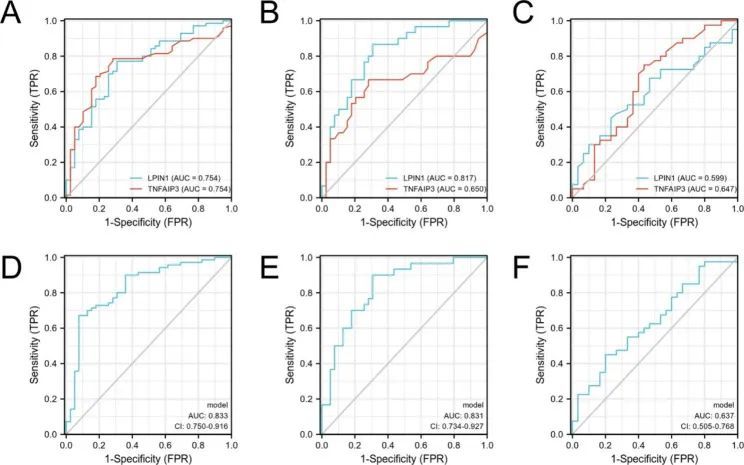
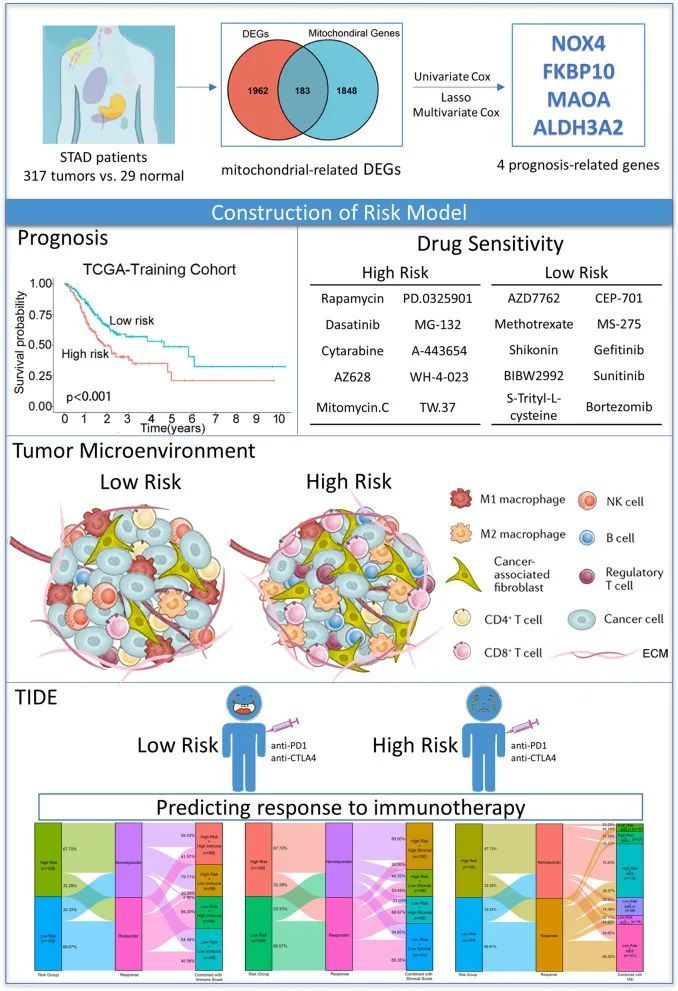
7+线粒体相关基因预后模型+肿瘤微环境+免疫细胞浸润+实验验证
今天给同学们分享一篇线粒体预后模型实验的生信文章“Constructing a novel mitochondrial-related gene signature for evaluating the tumor immune microenvironment and predicting survival in stomach adenocarcinoma”,这篇文章于2023年3月13日发表在J Trans…
10+家族基因+泛癌+空间转录组生信思路
今天给同学们分享一篇家族基因泛癌空间转录组的生信文章“A pan‐cancer blueprint of genomics alterations and transcriptional regulation of Siglecs, and implications in prognosis and immunotherapy responsiveness”,这篇文章于2023年5月23日发表在Clin T…
Platypus 一种集中式的央行数字货币方案
集中式的CBDC,混合使用账户模型和UTXO模型。
角色分类
中央银行:发行货币,交易验证,公开交易日志,防止双花。
不是完全受信任的,假定为会遵守监管要求,但可能会破坏交易隐私,即获…
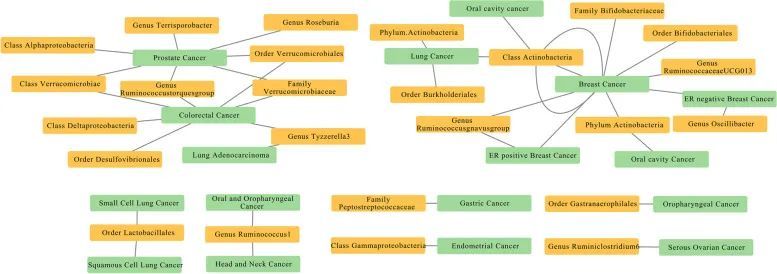
11+肠道微生物群+孟德尔随机化
今天给同学们分享一篇孟德尔随机化的生信文章“Causal relationship between gut microbiota and cancers: a two-sample Mendelian randomisation study
”,这篇文章于2023年2月21日发表在
BMC Med
期刊上,影响因子为11.15。 观察性研究和临床试验的…
知识管理软件那么多,怎么挑选才适合初创企业?
对于初创企业来说,资源有限,效率显得尤其重要。此时,一个强大的知识管理软件就显得必不可少。它不仅利于信息的录入、查找和共享,还可以帮助团队更好的组织和协作,提高工作效率。那么,在众多的知识管理软件…
ZKP价值链路的垂直整合
1. ZKP proof生命周期
从ZKP(zero-knowledge proof)生命周期,先看围绕ZKP的价值链路形成:
1)User intent用户意图:以某用户意图为起点,如想要在某zk-rollup上swap某token、证明其身份、执行某…
零知识证明:安全定义
之前在本科的课程仅仅略微介绍了下零知识证明,之后自学了一些相关内容,但不成体系。本学期跟着邓老师较为系统地学习了 ZKP,发现自己之前有很多的误解,临近期末整理下重要内容。
参考文献:
Goldreich O. Foundations…
安全多方计算之五:零知识证明(从入门到入土。。)
零知识证明1. 简介2. 零知识证明的例子2.1 向红绿色盲证明红球、绿球2.2 数独的零知识证明2.3 三染色问题的零知识证明2.4 Quisquater-Guillou 零知识协议3. ElGamal加密的零知识证明3.1 ElGamal加密的已知明文证明3.2 ElGamal加密的二选一零知识证明3.3 ElGamal加密的1-out-of…
2023海内外零知识证明学习资料汇总(二)(深入理解零知识证明篇)
工欲善其事,必先利其器
Web3开发中,各种工具、教程、社区、语言框架.。。。 种类繁多,是否有一个包罗万象的工具专注与Web3开发和相关资讯能毕其功于一役?
参见另一篇博文👉 2024最全面且有知识深度的web3开发工具、web3学习项目…
多重验证及比特币脚本中的P2PK、P2PKH、P2SH机制
在数字货币的世界中,安全性和有效性是核心要素。其中,二重验证作为一种强化账户安全的重要手段,以及比特币赎回脚本系统中的P2PK、P2PKH、P2SH等交易类型,对于理解区块链技术的底层逻辑和实现方式至关重要。本文将对这些概念进行深…
ZKP Understanding Nova (1): MinRoot Example
Understanding Nova
Kothapalli, Abhiram, Srinath Setty, and Ioanna Tzialla. “Nova: Recursive zero-knowledge arguments from folding schemes.” Annual International Cryptology Conference. Cham: Springer Nature Switzerland, 2022.
Nova: Paper Code
1. Unders…
8+铜死亡+分型+预后模型
今天给同学们分享一篇铜死亡分型预后模型的生信文章“Signature construction and molecular subtype identification based on cuproptosis-related genes to predict the prognosis and immune activity of patients with hepatocellular carcinoma”,这篇文章于2…
[持续更新]计算机经典面试题基础篇Day2
[通用]计算机经典面试题基础篇Day2
1、单例模式是什么,线程安全吗 单例模式是一种设计模式,旨在确保一个类只有一个实例,并提供全局访问点。通过使用单例模式,可以避免多次创建相同的对象,节省内存资源,同…
4. ZKP 程序实例及其相关资料汇总
Plonk demo Plonk Tutorial (对于vitalik博客的python实现) https://github.com/barryWhiteHat/plonk_tutorialdusk library:https://github.com/dusk-network/plonkdusk-demo: https://dusk.network/news/zero-knowledge-plonk-demo资料汇总 https://vitalik.ca/general/2019…
Lookup Singularity
1. 引言
Lookup Singularity概念 由Barry WhiteHat在2022年11月在zkResearch论坛 Lookup Singularity中首次提出:
其主要目的是:让SNARK前端生成仅需做lookup的电路。Barry预测这样有很多好处,特别是对于可审计性 以及 形式化验证ÿ…
3+单基因泛癌+铜死亡纯生信思路
今天给同学们分享一篇3单基因泛癌铜死亡纯生信思路的生信文章“Systematic pan-cancer analysis identifies SLC31A1 as a biomarker in multiple tumor types”,这篇文章于2023年3月27日发表在BMC Med Genomics 期刊上,影响因子为3.622。 溶质载体家族3…
计算机二级52条基础知识考点
1. 栈支持子程序调用。 2. 栈中插入元素的规则是“先进后出”或“后进先出”。 3. 队列的进出原则是“先进先出”。 4. 循环链表是另—种形式的链式存贮结构。 5. 线性结构包括—维数组、队列和栈。 6. 非线性结构包括 树、二叉树。 7. 数据的存储结构是指…
5+SUMO化修饰+分型+实验,经典生信思路
今天给同学们分享一篇5SUMO化修饰分型实验的生信文章“SUMOylation patterns and signature characterize the tumor microenvironment and predict prognosis in lung adenocarcinoma”,这篇文章于2023年4月13日发表在Front Cell Dev Biol 期刊上,影响因…
Sui主网升级至V1.11.2版本
Sui主网现已升级至V1.11.2版本,同时Sui协议升级至27版本。其他升级要点如下: 对于一些更高级别的交易,更改了一些gas费设置,使其gas费消耗的更快。这些更改不影响以前在网络上运行的任何交易,只是为了确保在开始大量使…
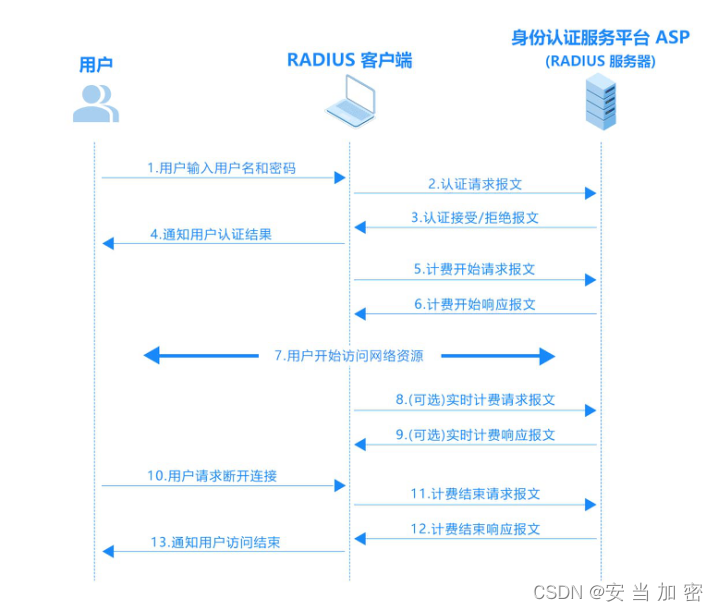
Radius OTP实现VPN登录认证 安当加密
实现Radius OTP认证来完成VPN登录,需要使用支持Radius协议的VPN设备和客户端,以及一个Radius服务器来处理用户认证。
安当ASP身份认证平台作为一个企业通用的身份认证系统,集成了Radius认证功能,可满足所有支持radius认证的设备登…
【区块链】科普:零知识证明、ZKRollup 与 zkEVM
译者语:2023 年将迎来 zkEVM 大发展,让我们看看有哪些项目在进行 zkEVM 的研究,zkEVM 可以做什么 原文链接: https://blog.pontem.network/zk-proofs-301-zksync-other-zkevm-b28641dc8565这篇文章让我们解释一下zkEVM是如何工作的,为什么它们是如此重要的创新。
长话短说…
Sui流动性质押黑客松|本周Workshop预告
Sui流动性质押黑客松正在如火如荼的报名中,Sui基金会现诚邀全球开发者前来参与,助力资产再流通。了解黑客松详情:Sui流动性质押黑客松开启报名,赢取千万美金质押和奖励!
黑客松官方网站:Sui Liquid Stakin…
国自然研究热点SUMO化如何开展研究?
今天给同学们分享一篇SUMO化修饰预后模型的生信文章“A novel risk model of three SUMOylation genes based on RNA expression for potential prognosis and treatment sensitivity prediction in kidney cancer”,这篇文章于2023年5月2日发表在Front Pharmacol期…
SGX:multi-prover的潜在解决方案
1. 引言
尽管ZK-Rollups、电路和SNARK非常复杂且不够成熟,但使用multi-prover方案可对冲证明系统、架构和实现中错误和漏洞的风险。
所谓mulit-prover是指:
多种不同类型的proofs。
multi-prover的实现:
可采用不同的证明类型࿰…
【每日一个知识点】你一般初始化多少线程数?
在网上有如下这样一个公式:
CPU 密集型,则线程池大小设置为 CPU 核数 1I/O 密集型,则线程池大小设置为 2 * CPU 核数 1
这里为什么要 1 呢?这样做主要是基于如下两个方面的考虑:
最大化CPU利用率:在理…
利用多核的Rust快速Merkle tree
1. 引言
利用多核的Rust快速Merkle tree,开源代码见:
https://github.com/anoushk1234/fast-merkle-tree(Rust)
其具有如下属性:
可调整为任意高度构建root复杂度为O(n)提供了插入和获取叶子节点的方法获取某叶子节…
8+纯生信,多组机器学习+分型探讨黑色素瘤发文思路。
今天给同学们分享一篇泛癌多组机器学习分型的生信文章“Comprehensive characterisation of immunogenic cell death in melanoma revealing the association with prognosis and tumor immune microenvironment”,这篇文章于2022年9月23日发表在Front Immunol 期刊…
Binius:助力ZK行业发展
1. 引言
前序博客:
Binius:基于binary fields的SNARKs(Part 1)
Zero-knowledge and validity proofs,通常简称为ZK,代表了密码学、数学和计算机科学领域的一个迷人领域。ZK允许一方,即Prover…
ZKP9 SNARKs based on Linear PCP (Pinocchio Groth16)
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 9: SNARKs based on Linear PCP (Yupeng Zhang) SNARKs learned so far Earliest Implemented SNARKs Pros Shortest proof size (3 elements [Groth16])Fast verifier (bilinear pairing) Cons FFT and group exponentiatio…
Sui第七轮资助:八个项目共获得超过50万美元的资助
今日,Sui基金会宣布了本月获得资助的项目方,他们将获得超过50万美元的资助金,用于构建项目,推动Sui的采用和发展。要获得资助,项目必须提交提案,详细说明他们正在构建的内容、预算明细、关键里程碑、团队经…
铜死亡+多组机器学习+WGCNA+分型
今天给同学们分享一篇铜死亡多组机器学习WGCNA分型的生信文章“Machine learning screening for Parkinsons disease-related cuproptosis-related typing development and validation and exploration of personalized drugs for cuproptosis genes”,这篇文章于20…
ZKP10.2 Efficient Recursion via Statement Folding (Nova)
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 10: Recursive SNARKs, Aggregation and Accumulation (Dan Boneh)
10.3 Efficient Recursion via Statement Folding: Nova, Supernova, and generalizations The difficulty with full recursion Prover P needs to build a…
ZKP16 Hardware Acceleration of ZKP
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 16: Hardware Acceleration of ZKP (Guest Lecturer: Kelly Olson) The What and Why of Hardware Acceleration Hardware acceleration is the use of dedicated hardware to accelerate an operation so that it runs faster…
如何利用chatgpt入门学习零知识证明?
Rust开源零知识证明算法有没有优秀的rust开源的零知识证明算法,是的,有很多优秀的 Rust 开源的零知识证明算法,以下是其中一些:bellman: 一个 Rust 实现的零知识证明库,它支持高效的 Groth16 零知识证明系统࿰…
8+肿瘤+多组机器学习+分型。
今天给同学们分享一篇肿瘤多组机器学习分型的生信文章“Integrated multiomics analysis and machine learning refine molecular subtypes and prognosis for muscle-invasive urothelial cancer”,这篇文章于2023年6月5日发表在Mol Ther Nucleic Acids期刊上&…
11+单基因泛癌,转录组+单细胞+机器学习+预后模型
今天给同学们分享一篇单基因泛癌多实验的生信文章“A transcriptomic pan-cancer signature for survival prognostication and prediction of immunotherapy response based on endothelial senescence”,这篇文章于2023年3月28日发表在J Biomed Sci期刊上…
探析零知识证明高能发展路径:走向更安全、私密且可扩展的 Web3 新时代
原文:https://www.coinbase.com/blog/understanding-the-zero-knowledge-landscape
作者:Jonathan King|Coinbase Ventures
编译:TinTinLand 本文核心观点
2023 年,零知识技术吸引了逾 4 亿美元的投资,主…
ZKP6.3 Discrete-log-based Polynomial Commitments (Bulletproofs)
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 6: Discrete-log-based Polynomial Commitments (Yupeng Zhang)
6.3 Bulletproofs and other schemes based on discrete-log KZG: Pros: Commitment and proof size: O(1), 1 group elementVerifier time: O(1) pairing Cons…




































![[2024区块链开发入门指引] - 比特币运行原理](https://img-blog.csdnimg.cn/img_convert/679a4160ce14887093a56d47d4e30d01.jpeg#pic_center)